| Author |
Message |
Todd Wasson (Todd_wasson)
New member
Username: Todd_wasson
Post Number: 10
Registered: 4-2003
| | Posted on Monday, May 05, 2003 - 5:28 pm: | |
Right, Mark :-)
On another note for everyone, I went ahead and asked a licensed mechanical engineer to take a look at Efwun's post and see if he could point out where the simple f=ma thinking might be wrong. Here's his reply:
"Here's where I think he summarizes his viewpoint:
"F=MA works only in the construct of the application of a force as in an
inelastic collision, because if that force is more than the instantaneous
overcoming of inertia, there would be an increasing rate of acceleration,
and distance and time become factors. Remember, F*D =Work."
The part about F=MA is meaningless gibberish--F=MA works just fine, but F
and A are instantaneous values.
"Therefore, one physical construct that works for acceleration over distance
and time is the change in kinetic energy of the vehicle, or W=delta KE."
This isn't really true, because it takes power just to hold the vehicle at
constant speed.
"Then, it follows without arcane manipulation that Delta KE/time=W/Time or
POWER."
With the caveat that the power he cites is average power and the one above,
I can't disagree, except to say that acceleration, strictly defined, is an
instantaneous quantity and Delta KE is net power integrated over a finite
stretch of time.
"Let me finish by stating that my final understanding of this conundrum is
that a motor that can hold within percentage points of its torque peak as
revolutions ascend will accelerate hardest at the point where ascending
revolutions optimally intersect with descending torque. Those vehicles
accelerate hardest well above torque peak, perhaps even at "power" peak.
Vehicles with steeply descending torque curves reach that optimal
combination of torque and revolutions much earlier, and therefore accelerate
hardest closer to, or at, torque peak. Remember, torque is the measured
resistance on a dyno, while power is that output calculated as the ability
to accomplish a set amount of work in a discrete amount of time."
This is a lot of hand-waving and BS where he should be using mathematics.
He doesn't say whether he's talking about acceleration in a particular gear
or the best acceleration you can get at a particular speed. It's true that
with a steeply descending torque curve, the power peak is not far from the
torque peak, and that a relatively flat torque curve can have the power peak
at much higher revs than the torque peak. However, his presentation is
confused and vague, and misses the essential point.
"Therefore, P=W/T= Delta KE works for all situations, and explains why some
cars accelerate hardest near torque peak, and why some accelerate hardest at
power peak and the vast majority are somewhere in between. To reiterate, "it
depends." "
I don't think he remotely succeeds in explaining what he claims to explain.
What accelerates a car is thrust force at the drive wheels. Given constant
percentage power loss in the drive line, max thrust occurs at maximum power,
and shifting should occur where the power available in the next gear equals
power in the gear you're in (because it's on its way down in the lower gear
and on its way up in the next gear up). But, in any particular gear, the
max acceleration happens at the torque peak.
I hope that helps.
"
(name snipped)
Score one more for simplicity, guys. ;-)
Todd Wasson
Performance Simulations
Drag Racing and Engine Simulation Software
http://performancesimulations.com
|
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 618
Registered: 4-2002
| | Posted on Monday, May 05, 2003 - 5:28 pm: | |
Long ago in this thread, it was indicated and confirmed that with a CVT max acceleration coincides with max HP. That is why this discussion is replete with notations like "in any gear". |
Mark Eberhardt (Me_k)
Member
Username: Me_k
Post Number: 490
Registered: 5-2002
| | Posted on Monday, May 05, 2003 - 11:50 am: | |
Mike,
With a continuously variable transmission, the engine would go to peak HP and stay there to accelerate the car the fastest and obtain max speed. Here�s a quick example of why.
If you have an engine that makes 200 ft-lbs torque at 5000 rpm and 250 HP at 7500 (175 ft-torque). For some speed the drive ratio is 3:1, so with the engine at 5000 rpm, 600 ft-lbs torque gets to the wheels. At the same speed you could down shift the a 4.5 ratio and bring the engine to 7500, that would put 787 ft-lbs torque to the wheels. Clearly much better.
If the point is to accelerate the car, maximizing the area under the HP curve yields the best result, which in may cars means you are always above the torque peak (except 1st gear where you pull through it).
|
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 613
Registered: 4-2002
| | Posted on Monday, May 05, 2003 - 10:01 am: | |
"fengine-fair=0"
An interesting point about forces and power;
While the force required to push against air increases with the square of speed (fair = 1/2*rho*v**2), the power increases with the cube:
p/v = f = m*a
p = f*v
p = 1/2*rho*v**3
This also annotates a difficulty in menal conception of the problem: acceleration is caused by the sum of forces applied, not the sum of powers, or the sum of energies.
So why do we choose a gear that achieves top speed at (about) max power? Because gear multiplication allows the car to continue accelerating up to the point where the HP produced is equal to the HP available. Since there is more power at max HP than at max TQ, acceleration will continue (albeit at reduced rate). These are really two different kinds of problems.
*Where rho is the viscocity of the fluid medium: in this case air. "Race car aerodynamics: designing for speed" Joseph Katz chapter 3. |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 530
Registered: 6-2002
| | Posted on Monday, May 05, 2003 - 9:37 am: | |
Its taken me 500 posts, but I believe Todd has finally "illuminated" the answer.
First fact: Gearing acts as a torque multiplier.
Second fact: Max speed will be achieved when max RPM in longest gear is achieved. (Hard mechanical link between engine turning and wheels turning).
Third fact: As a result of torque multiplication, more RPM can be achieved (more speed) even though the engine is not at max torque. It is a question of where the "curves cross," that of diminishing torque against gear/torque multiplication.
Fourth fact: Power is the amount of work that can be done in a unit of time. At max speed, the most work is being done (max force multiplied by max distance). Gear/torque multiplication is mechanical advantage, not unlike a multi-pulley system. More RPMs (rope distance) must be turned to accomplish the same work. At max horsepower, this is optimized.
End of story (for me, anyway).
Jim S. |
Todd Wasson (Todd_wasson)
New member
Username: Todd_wasson
Post Number: 9
Registered: 4-2003
| | Posted on Monday, May 05, 2003 - 3:22 am: | |
Good one, Mike :-)
An easy way to think about or remember this acceleration stuff is:
1. Pick a speed (mph). Any speed. Your maximum acceleration (and force at the driving wheels) will occur if you gear the car to put the engine at peak power at that speed. (Remember, what really counts is engine torque times gear ratio; i.e., torque at the driving wheels, so if you can double the gear ratio and your engine torque only drops off 10%, you're way ahead of the game.)
2. Pick a gear and stay in that gear. Max acceleration is at peak torque, because that's where the engine is producing the most twisting force.
What about top speed? You'll have more force if the car is geared to put the engine at peak power at the speed you're interested in. This follows #1 above. The most driving force is available at that point.
f=ma is all that's needed here. Calculus can be left at the door on these simple problems.
Todd Wasson
Performance Simulations
Drag Racing and Engine Simulation Software
http://performancesimulations.com
|
Mike B (Srt_mike)
Junior Member
Username: Srt_mike
Post Number: 168
Registered: 12-2002
| | Posted on Sunday, May 04, 2003 - 11:52 pm: | |
James,
You forget the laws of thermodynamics. You realize, of course, that any system will at some point reach equilibrium, right? You have four Ferraris and I have none. Physics dictates that you must give me two of them. You can choose which, as long as one is the TR.
As for the question at hand, if you had an infinitely variable transmission, max speed would be at torque peak, IMO. However since that isn't how our cars work, the car is trying to rev higher but not lose so much torque (in order to achieve max speed). Torque at RPM's is horsepower. Therefore it's HP that is required to attain top speed. Correct me if I am wrong, someone. |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 529
Registered: 6-2002
| | Posted on Sunday, May 04, 2003 - 10:59 pm: | |
Kristoffer - thank you. As an engineering student, you will understand the mass/flow equation in my garage. I tend to acquire, but not sell.
Mark - read my last post. I understand what you are suggesting, but irregardless of gearing, max speed will be achieved when there is a maximum force pushing the car. Acceleration is that dynamic of a car that is left when air resistance is exceeded by tire force. The car will continue to accelerate as long as the force pushing it forward exceeds forces pulling it backwards (resistance, rolling resistance, etc.) Thus, it is at max speed when these forces balance.
Help me here.
Jim S. |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 528
Registered: 6-2002
| | Posted on Sunday, May 04, 2003 - 10:51 pm: | |
Mark - now I understand your post. However, it brings us full circle to the initial question. Irrespective of gearing, for the same engine and gear box, won't maximum force at the tire/asphalt interface be seen at maximum torque?
Wait. Wait. Wait. Incoming brain F**T. The ability to do the most work for each revolution of the tire (force multiplied by distance in the shortest period of time) will occur at max horsepower. There is more to this thought, but I do not wish to create a long post.
Jim S. |
Mark Eberhardt (Me_k)
Member
Username: Me_k
Post Number: 489
Registered: 5-2002
| | Posted on Sunday, May 04, 2003 - 5:39 pm: | |
Jim,
I think we're talking about different things. My post was related to peak acceleration, which is 0 at the torque/drag balance point. Although max acceleration is obtained at the torque peak in every other case, max speed is obtained at the torque peak if and only if the gear ratios used produce a torque/drag balance at the torque peak. If top speed is what you are after, selecting gearing that allows you to get to your HP peak will produce the highest number. |
Kristoffer Hansson (Maverick)
Junior Member
Username: Maverick
Post Number: 97
Registered: 3-2001
| | Posted on Sunday, May 04, 2003 - 5:16 pm: | |
Hey James - Thats a lovely collection of f-cars you have! |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 522
Registered: 6-2002
| | Posted on Sunday, May 04, 2003 - 4:38 pm: | |
Kristoffer - I stand corrected. Thank you.
Jim S. |
Kristoffer Hansson (Maverick)
Junior Member
Username: Maverick
Post Number: 93
Registered: 3-2001
| | Posted on Sunday, May 04, 2003 - 4:19 pm: | |
faisol - lmao
I havent followed this thread at all but beeing a student of engineering in science:
James - Actually, wind resistance isnt proportional to the square. Maybe we can approximate it to the square at certain speeds. But the thruth is that the resistance goes up with the speed. In really high speeds its more like the cube and in low speeds the resistance is more like linear.. But for the rest youre ofcourse on the head.
|
Faisal Khan (Tvrfreak)
Junior Member
Username: Tvrfreak
Post Number: 87
Registered: 3-2003
| | Posted on Sunday, May 04, 2003 - 4:07 pm: | |
But mass increases, as the bugs on the front pile up. This leads to less torque, as additional mass now needs to be propelled.
Accordingly, VW bugs are the fastest. |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 521
Registered: 6-2002
| | Posted on Sunday, May 04, 2003 - 1:18 pm: | |
Mark - the car continues to accelerate until the forces are balanced, i.e., wind resistance equals torque (force) at the tire/asphalt interface. Wind resistance grows with the square of velocity, thus, slightly below maximum speed, wind resistance is less. When maximum speed is achieved, we have a stalemate between force vector from tires and the negative wind resistance vector. Accordingly, maximum speed does occur at maximum torque.
Jim S. |
Mark Eberhardt (Me_k)
Member
Username: Me_k
Post Number: 488
Registered: 5-2002
| | Posted on Sunday, May 04, 2003 - 9:11 am: | |
Mitch,
As usual, everything you posted look exactly right. I think a small clearification is need though as the car approaches it's maximum speed, where fengine-fair=0. If this occurs at torque peak, then acceration is 0 at the torque peak, so it must have been maxium below the torque peak. That's the only case I can think of that it's not at the torque peak. |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 609
Registered: 4-2002
| | Posted on Friday, May 02, 2003 - 5:45 pm: | |
OK, lets do it EFWUNs way:
w=f*d // definition of work
p=w/t // definition of power
Combining above equations:
p=f*d/t
Remembering that v=d/t we get:
p=f*v
p/v = f
So, the power being produced divided by the current velocity causes the force that accelerates the car. But wait:
E=1/2*m*v**2
dE/dt= m*v*dv/dt
and remembering that dv/dt = a
dE/dt = m*v*a
But since:
dE/dt = p // another definition of power
we get:
p=m*v*a
and rearanging:
p/v = m*a
confirming f=m*a, and p/v=f.
This set of equations is complete, even stating at work! But if you insist, you can write:
a=p/(v*m)
However, when you differentiate this to find the point of maximum acceleration:
da/dt = 1/m*d(p/v)/dt
da/dt = 1/m*(-p/v**2*dv/dt + 1/v*dp/dt)
Solving for point of maximum acceleration:
da/dt=0
0= 1/m*(-p/v**2*a + 1/v*dp/dt)
some quick algebra:
a*p/v**2 = 1/v*dp/dt
a*p/v = dp/dt // at the point of maximum acceleration
If dp/dt was 0, then we would be at maximum HP, but since all the terms in (a*p/v) are greater than zero, then (a*p/v) has to be greater than zero, therefore, we cannot be at the point of maximum HP. Therefore, the point of maximum acceleration cannot correspond to the point of maximum HP. Since we cannot be at max HP, lets solve this to see where we are;
a=p/(v*m) // restating acceleration based on power
m*a = p/v
maximum acceleration occurs when da/dt = 0:
m*da/dt = d(p/v)/dt
since we know: f=m*a, we must nessarily know p/v=f=m*a.
0 = m*da/dt = df/dt
Therefore df/dt iszero at the point of maximum acceleration. The place where df/dt is zero is (((drum roll))) peak torque.
EFWUNs argument that the equasion of work leads to a different conclusion has therefore shown to be false. Q.E.D. |
PSk (Psk)
Member
Username: Psk
Post Number: 415
Registered: 11-2002
| | Posted on Friday, May 02, 2003 - 4:19 pm: | |
Guys,
Give it up, you will never ever get EFWUN to change his incorrect views. I mean this with the utmost respect EFWUN but come on, how many people and very knowledgable people have to prove that F=m.a is all that is required and that Torque is it, before you will change your views.
Many times in my life I have been wrong, but you only move forward if you are prepared to listen to others.
F=m.a works in all situations, even with air resistance as the air resistance simply works as an opposing force ... calculating how much force that is applied at a particular point is the interesting part but F=m.a still holds.
A car, even though it has a different type of engine, still abides by all laws of physics and the F=m.a formula.
Your professor friend will confirm this when he actually sits down and does the calculations ...
Mitch,
That paper you posted is extremely interesting and very clear and the section near the end where they are calculating speeds on a race track straights confirms 100% that this issue is closed.
Have a good day all.
Pete |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 296
Registered: 3-2002
| | Posted on Friday, May 02, 2003 - 4:05 pm: | |
EFWUN: "Brian, I've tried to be polite about this, you don't seem constrained by the same rules."
I don't see anything impolite in my post. I simply stated the well-known, indisputable facts.
EFWUN: "Simply put, F=MA works in a closed system with no wind resistance and for an object that isn't gaining kinetic energy as a square function of velocity."
And it also works in a system with wind resistance (which is an additional force that must be accounted for) and for an object gaining or losing kinetic energy (no need for any compensation whatsoever).
F=ma is a fundamental law of nature... its a fundamental truth that is beyond dispute... it is true in all situations.
EFWUN: "KE=1/2MVsquared is absolutely a fundamental truth."
Yes, just like F=ma, both are fundamental laws of nature.
EFWUN: "W=1/2M V final squared minus 1/2 MV initial squared. Another Newtonian truth."
Yep, where W is the work required to change the velocity from V[initial] to V[final].
EFWUN: "Torque*Distance/time = Power equals W/time, or Delta KE/t. Another Newtonian truth.
To create A at higher KE takes increasing torque*distance equal to 1/2velocity squared. Therefore, Force=Torque, F1=MA1 at 30kph, F1 CANNOT equal MA1 at 50kph."
Huh? You were doing good right up to here, where you started misapplying the math. I started to create an example to illustrate your error, but then you followed with a perfectly good example to use... so, I'll just use your example...
EFWUN: "Take this to an extreme for example. Will the exact same force that creates an acceleration of 5meters/sec-squared acting on Mass M at 0meters/sec create the exact same acceleration of Mass M at 100meters/sec? Absolutely NOT."
Absolutely SO! F=ma is true independent of velocity. You are simply doing your math wrong.
Let's perform your suggested experiment for 1 s (to keep you out of calculus) at each of the two velocities:
F = M * 5 m/s^2 is applied to both objects for 1 second. Both objects increase velocity 5m/s. The first starts at 0m/s and ends at 5m/s.
The second starts at 100m/s and ends at 105m/s.
The delta KE of each is thus:
dKE[1] = M/2 * (( 5m/s)^2 - ( 0m/s)^2) = M * 12.5 m^2/s^2
dKE[2] = M/2 * ((105m/s)^2 - (100m/s)^2) = M * 512.5 m^2/s^2
F=ma tells us the acceleration will be the same in both cases. KE=1/2 mv^2 tells us the energy increase will be much greater in the latter case. With me so far?
Thus, at the higher velocity, much more work had to be performed in order to apply that same force for that same 1s. No surprise there, since you'll obviously be applying the Force for a much greater distance when at a much greater velocity. To check those numbers, let's compute the work that was applied. W = FD.
In both cases, F = M * 5m/s^2.
The distances the force F was applied are:
D[1] = 1s * ( 5m/s + 0m/s)/2 = 2.5m
D[2] = 1s * (105m/s + 100m/s)/2 = 102.5m
so, the work (W=F*D) in each case is:
W[1] = M * 5m/s^2 * 2.5m = M * 12.5 m^2/s^2 = dKE[1]
W[2] = M * 5m/s^2 * 102.5m = M * 512.5 m^2/s^2 = dKE[2]
How about that! The work applied exactly equals the increases in kinetic energy due to the identical accelerations... which were far more simply computed using F=ma.
And using your own "extreme example", we have illustrated that 'F=ma' works perfectly independent of starting and ending velocities.
I don't think I can make it any more "plain and simple".
|
victor v villarreal (Vvvmd)
New member
Username: Vvvmd
Post Number: 24
Registered: 1-2003
| | Posted on Friday, May 02, 2003 - 3:34 pm: | |
EFWUN
Please pay attention. Lbft of torque has units of mass time and distance. Lb(force) and lb(mass) have the samevalue at sea level on the planet earth. One lb(force) is defined as the amount of force required to accelerate one lb(mass) at a rate of 32.174 ft/sec^2. One lb(force) is equal to 4.45 Newtons. One Newton has units of kgm/sec^2. Lb(force) also have units of mass times distance devided by time squared. These are basic definitions. You continue to argue that torque cannot cause acceleration because it has no units of time or distance. You are wrong! Please go look this up in a high school physics book before you make such a statement again. Once you accept this definition you will see that torque produces the force at the tire contact patch that pushes the car forward. If you cannot understand that torque is a force that has units of time distance and mass then you have shown you don't have the basic understanding of the language of physics. If you can't understand the language you can't understand the priciples of force work and power and how they affect acceleration and speed. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 629
Registered: 2-2003
| | Posted on Friday, May 02, 2003 - 1:59 pm: | |
Mr. Alsup:
Succinctly, the acceleration of a motor vehicle with a motor that creates a rotational output does not come from torque, because torque has no component of distance or time.
Acceleration comes from Torque*Distance which equals W and results in Delta Kinetic Energy. To analyze the effect of that work in increasing Kinetic Energy as a function of time, we should analyze Torque*Distance/time, or Power.
If to maintain Acceleration equal to "A", Power must increase as a function of 1/2Velocity-squared, how can you not admit that F must similarly increase? In fact, F=MA cannot answer this conundrum, but must be combined with other physical equations the truth of which you and I have proven, succinctly, those equations are KE=1/2mv-squared, and d=1/2aT-squared.
You insist that calculus must be employed so as to allow the use of F=MA. Simply put, where the system under investigation is a dynamic system with increasing kinetic energy, you cannot simply graph instantaneous points of A as the result of force F, because there is more to the inquiry.
The reason that equations are derived from the fundamental laws of physics is to encompass situations where more variables are necessary.
To review, please notice that P=W/time, and W=Force (torque) *Distance. Therefore, increasing power IS the expression of increasing Force over the same interval of distance and time.
If we agree that PT equals �mv final squared minus � mv initial squared, then the following values obtain for intervals between 30kph and 35kph, and 50kph and 55kph.
PT=� M (9.72meters/sec)squared -minus- � M (8.33meters/sec) squared (30-35kph)
PT=� M(15.27meters/sec)squared -minus- � M (13.89 meters/sec) squared(50-55kph)
Thus, PT= � M(94.5) minus � M (69.39); and
PT= � M(233.17) minus � M (192.92);
Therefore, assuming M equal to 1;
PT= 12.56 for 30-35kph
PT= 22.125 for 50-55kph.
Let�s make T equal to 1second, and we have
P=12.56 for 30-35kph; and
P= 22.125 for 50-55kph.
Therefore, to create the same acceleration, 5kph/sec squared, we need 22.125/12.56 as our differential P.
Thus differential P2 must be 1.762 times P1. I submit that there are many examples of motors that make twice the power at peak power than they do at peak torque, and therefore, in the speed range demonstrated above, they accelerate faster at peak power than at peak torque. Others do not, and those vehicles will fall somewhere in the range between peak torque and peak power. Finally, some motors fall rapidly off the torque curve as rpm climbs, and these cars will accelerate most rapidly at or near peak torque.
P=Delta KE/t cannot be disproven, and is the best beginning for an inquiry into a complex system where a motor vehicle is accelerated as a changing function of distance and velocity.
You have stated previously that "torque creates low velocity acceleration, while power is necessary to overcome increasing wind resistance." Now add the necessity of investigating increasing kinetic energy of the system, and you begin to see the complexity of this inquiry.
Simply put, acceleration will peak at the optimal intersection of increasing Kinetic Energy and increasing Power; in some cars "within spitting distance" of torque peak, in others "within spitting distance" of power peak. It depends how quickly torque falls off as revs rise.
Succinctly, "it depends." |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 608
Registered: 4-2002
| | Posted on Friday, May 02, 2003 - 12:44 pm: | |
"Okay, then how can the same Force-1 acting on Mass-1 that creates A-1 at 30Kph create the same acceleration A-1 acting on Mass1 at 50Kph?? Answer, It cannot."
Real answer: (ignoring air resistance) if you apply a force F1 on an object of mass M1 you will get an acceleration of A1 = F1/M1 that is independent of the speed of the object when the force is applied. This works equally well at 30 MPH as it does at 50 MPH or 2MPH.
However, the power required to cause this acceleration increases linearly with speed P = f*v.
"Simply put, F=MA works in a closed system with no wind resistance and for an object that isn't gaining kinetic energy as a square function of velocity."
When you want to consider air resistance you write the equation as:
(Fengine-Fairresistance) = M*a
The sum of the forces involved (engin being positive and air resistance being negative) cause the acceleration. Not understanding that F in f=M*a is the total of all the forces (in vector form) shows that your misunderstanding of this issue runs very deep. In sum, you are not educated in physics.
"KE=1/2MVsquared is absolutely a fundamental truth. An real object cannot gain velocity without gaining Kinetic Energy as the square function of velocity."
This also leads to f=M*a as has been shown countless times already. the fact is that you don't understand the physics. This is not a problem of physics anymore, it is a problem with your education!
"To create A at higher KE takes increasing torque*distance equal to 1/2velocity squared. "
Exactly--acceleration comes from TORQUE--just as you state. And that is why f=M*a works!
"Therefore, Force=Torque, F1=MA1 at 30kph, F1 CANNOT equal MA1 at 50kph."
It does if the TQ available at 50mph/kph is the same as the TQ at 30mph/kph!
"Will the exact same force that creates an acceleration of 5meters/sec-squared acting on Mass M at 0meters/sec create the exact same acceleration of Mass M at 100meters/sec? Absolutely NOT."
Here you are wrong--again. If the force acting upon a body is the same, then it WILL accelerate at the same rate independent of speed (neglecting air resistance).
"Therefore, the inquiry must subsume Kinetic Energy, (and wind resistance too) and that equation must start with
F*D=W and W/t= P=Delta KE/t. Plain and simple."
And this leads (when solved by people who can do math and physics) to the same conclusion as f=M*a.
-------------------------------------------------
Aside: people reading this thread may have wondered about my capatalization of various letters in equations. In comon physics usage, when a variable is constant it is represented with a capatalized letter, if it changes it is represented without a capatal. So writing f=M*a denotes that mass is a constant here, while f and a are variables. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 628
Registered: 2-2003
| | Posted on Friday, May 02, 2003 - 10:54 am: | |
To quote Mr. Alsup
"So the power required to accelerate rises linearly with speed."
Okay, then how can the same Force-1 acting on Mass-1 that creates A-1 at 30Kph create the same acceleration A-1 acting on Mass1 at 50Kph?? Answer, It cannot.
Simply put, F=MA works in a closed system with no wind resistance and for an object that isn't gaining kinetic energy as a square function of velocity.
KE=1/2MVsquared is absolutely a fundamental truth. An real object cannot gain velocity without gaining Kinetic Energy as the square function of velocity.
Our hypothetical vehicle is a real object, gaining kinetic energy as the square of velocity, and that kinetic energy must come from the work that is increasing the velocity and imparting that kinetic energy.
W=1/2M V final squared minus 1/2 MV initial squared. Another Newtonian truth.
Torque*Distance/time = Power equals W/time, or Delta KE/t. Another Newtonian truth.
To create A at higher KE takes increasing torque*distance equal to 1/2velocity squared. Therefore, Force=Torque, F1=MA1 at 30kph, F1 CANNOT equal MA1 at 50kph.
Take this to an extreme for example. Will the exact same force that creates an acceleration of 5meters/sec-squared acting on Mass M at 0meters/sec create the exact same acceleration of Mass M at 100meters/sec? Absolutely NOT. Therefore, the inquiry must subsume Kinetic Energy, (and wind resistance too) and that equation must start with
F*D=W and W/t= P=Delta KE/t. Plain and simple.
|
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 627
Registered: 2-2003
| | Posted on Friday, May 02, 2003 - 10:42 am: | |
Brian, I've tried to be polite about this, you don't seem constrained by the same rules.
Simply put, F=MA works in a closed system with no wind resistance and for an object that isn't gaining kinetic energy as a square function of velocity.
KE=1/2MVsquared is absolutely a fundamental truth. An real object cannot gain velocity without gaining Kinetic Energy as the square function of velocity.
Our hypothetical vehicle is a real object, gaining kinetic energy as the square of velocity, and that kinetic energy must come from the work that is increasing the velocity and imparting that kinetic energy.
W=1/2M V final squared minus 1/2 MV initial squared. Another Newtonian truth.
Torque*Distance/time = Power equals W/time, or Delta KE/t. Another Newtonian truth.
To create A at higher KE takes increasing torque*distance equal to 1/2velocity squared. Therefore, Force=Torque, F1=MA1 at 30kph, F1 CANNOT equal MA1 at 50kph.
Take this to an extreme for example. Will the exact same force that creates an acceleration of 5meters/sec-squared acting on Mass M at 0meters/sec create the exact same acceleration of Mass M at 100meters/sec? Absolutely NOT. Therefore, the inquiry must subsume Kinetic Energy, (and wind resistance too) and that equation must start with
F*D=W and W/t= P=Delta KE/t. Plain and simple.
|
rich (Dino2400)
Junior Member
Username: Dino2400
Post Number: 208
Registered: 10-2001
| | Posted on Friday, May 02, 2003 - 10:42 am: | |
"With any luck, they will lock you up and this thread can end."
--
Mitch, you were doing so well! Minor slip aside, I like your new "just the facts" approach. |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 603
Registered: 4-2002
| | Posted on Friday, May 02, 2003 - 10:24 am: | |
Brian: and then there is the derivation:
E = 1/2*M*v**2
dE/dt = M*v*a= P
P/v = M*a
P/v = f
So the power required to accelerate rises linearly with speed
"F=MA has no ability to evaluate Kinetic Energy of the system."
Why not just integrate acceleration (a=f/M) into v and use E=1/2*M*v**2. Thereby a single step of calculus and you CAN convert acceleration into velocity, and we have a direct relationi between velocity and energy.
"acceleration WITHOUT EVALUATING EXPONENTIALLY INCREASING KINETIC ENERGY."
This is a statement so riddled with false physics it takes my breath away.
1) Exponentially Increaseing function have the form const**variable (call it K**x)
2) the functions we are looking at have the forms
x**K (where K is 0, 1, or 2)
3) the mathematical difference between exponential functions and simple physics is simply ENORMOUS.
4) the media is fond of using the word exponential, and 99.44% of the time is wrong in its use of the word.
5) your use of thie word exponential is also wrong.
6) the fact you don't understand this is a key ingreedient as to why you don't understand acceleration.
"Therefore, the NECESSARY evaluation must be Power = delta KE/t. I�ll post more later, must get to Court. "
We did this, it arrives at the same answer as f=M*a.
With any luck, they will lock you up and this thread can end. |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 295
Registered: 3-2002
| | Posted on Friday, May 02, 2003 - 8:34 am: | |
EFWUN states: "F=MA cannot describe our system of a vehicle accelerating through distance and time because that vehicle has Kinetic Energy increasing as the square of velocity, (KE=1/2 Mvsquared), and F=MA has no ability to evaluate Kinetic Energy of the system. "
Nice theory... too bad its just plain wrong. F=ma is true no matter what the kinetic energy of the object is. Consider for a moment that your cars travelling 30kph and 50kph are, in fact, hurling through space at many, many times that speed (planet Earth is hauling ass around the Sun which is, itself, hauling ass around the Milky Way, which is itself hauling ass. All of that tremendous kinetic energy is absolutely irrelevant in computing how a mass is accelerated by a force. Newtonian physics 101.
EFWUN continues: "If we posit F1=MA1 at 30KPH, how can we say that F1=MA1 at 50kph??"
Uhh, because its a fundamental law of physics.
"We cannot, simply because system at 50KPH has KE increased as the square of (50)squared minus (30) squared. F=MA has only Force without distance or time, Mass (weight and gravity) and resultant acceleration WITHOUT EVALUATING EXPONENTIALLY INCREASING KINETIC ENERGY."
But the law tells us that is irrelevant. The acceleration will equal the force applied divided by the mass... no matter how that causes the energy of the system to change. This really isn't a subject of opinion... its well-established fact... and quite literally one of the most basic physics concepts there is.
|
DES (Sickspeed)
Advanced Member
Username: Sickspeed
Post Number: 3800
Registered: 8-2002
| | Posted on Friday, May 02, 2003 - 8:27 am: | |
Can we get an update on the office pool and if there's still room for me to get in on it...?
Also, does anyone care to take/place/wager bets on who will emerge from this thread victorious...?
EFWUN, i have a certain "indicator" on my car that you might find useful to tis discussion; didn't really think about it until the other day... Email me if you think any kind of an indicator on a vehicle might be of any relevance to you and the points you're trying to make...  |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 625
Registered: 2-2003
| | Posted on Friday, May 02, 2003 - 7:41 am: | |
Gentlemen, please join me in considering this problem analytically.
F=MA cannot describe our system of a vehicle accelerating through distance and time because that vehicle has Kinetic Energy increasing as the square of velocity, (KE=1/2 Mvsquared), and F=MA has no ability to evaluate Kinetic Energy of the system.
If we posit F1=MA1 at 30KPH, how can we say that F1=MA1 at 50kph?? We cannot, simply because system at 50KPH has KE increased as the square of (50)squared minus (30) squared. F=MA has only Force without distance or time, Mass (weight and gravity) and resultant acceleration WITHOUT EVALUATING EXPONENTIALLY INCREASING KINETIC ENERGY. (We must have the "energy" from somewhere to put into that system!)
Therefore, the NECESSARY evaluation must be Power = delta KE/t. I�ll post more later, must get to Court. |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 602
Registered: 4-2002
| | Posted on Thursday, May 01, 2003 - 10:57 pm: | |
page 12 in:
http://www.miata.net/sport/Physics/phor.pdf
Should set EFWUN straight. (But I won't hold my breath) |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 600
Registered: 4-2002
| | Posted on Thursday, May 01, 2003 - 10:27 pm: | |
I spent some time and found a pretty good singular explanation fo the situation.
http://www.stanford.edu/~voloshin/lhowwhy.html
Wade down through the paper until you get to the section: "What gives you the rush". The gentleman works out the same set of equations I did 200 posts earlier. He then talks about power, work, drag and air resistance. Same equations I used.
Here is another physics of cars paper:
http://www.etse.urv.es/EngInf/assig/si2/cardynamics.pdf
http://www.wprince.com/physicsofracing/pdfs/part6.pdf
"Mr. Alsup, your post proves the point that it depends. You are assuming certain values for P, but you're not stating the corrolary, to wit; there is a point on the continuum between your example of 268hp, and 380hp where Power curve intersects increasing KE curve, and THAT is the point at which acceleration is maximum."
We have shown this is not the case at all. First we showed that the point of peak acceleration is coincident with the point of peak TQ.
"Mr. Alsup, again, you're not taking the time to read a post that disagrees with your own. The equation P=Delta KE/t is true, and is derived from other physical truths, to wit: F=MA, KE=1/2mv squared etc. P=Delta KE/t yields the results I've posted, and they show that "it depends." "
Not only do I take the time to read them, I take the dime to understand them and develop alternate solutions that agree with the other physical ways of determining solutions to these kinds of problems.
SO, lets say that you are right, why do all the other ways of setting up the equations end up pointing to peak acceleration occurs at peak TQ? Should not all ways of solving these problems agree on the solution? And if all way to solve the system of equations arrive at the same conclusion should we not use the simplest and most direct?
No, it is you who cannot see the futility of your position; not I. The math, the physics, the web references back up my claim. Nothing substantial (yet) backs up your claim.
"Similarly, if P was 220hp at P1, and P2 was 405hp, then the car accelerates more quickly right at power peak, illustrating the point, "it depends.""
If P was only 220 HP at P1 (30 MPH) and 405 HP at P2 (50 MPH), then P1 could not be peak TQ! so its not the point I am talking about.
220 HP at 30 MPH -> 7.33 units of TQ
405 HP at 50 MPH -> 8.10 units of TQ
So the point of 220 HP is not the point of peak TQ, so I dont care about P1, I care about the point where TQ is greatest because thats where acceleration is greatest. And, thereby, your example is nonillustrative!
"F*D=W, and W/time =Power=Delta KE/t, therefore 2Pt=mv final squared - mv initial squared. When we plug in values for those, as I did in my recent posts, we get a rational explanation, which accords with observations, rather than a doctrinal F=MA, which does not accord with observations."
Who's 'we'. When people that can use a calculator plug in the numbers, their solutions agree with f=M*a. You plug in numbers and get a different conclusion. It does seem the deck is stacked against you.
"I'm going home to my car and my wife. Please understand that I'm not motivated by the wish to "beat" you, but rather to explain this conundrum to my satisfaction. "
Don't worry, you CAN'T win, the physics, and math are on the side of reality.
"That site is elementary high-school physics;"
Good, I picked it that way so you would have a chance of comprehending it. At least you know the high schoolers should be able to use physics. Why can't lawyers?
BTW did you disagree with their conclusion? |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 292
Registered: 3-2002
| | Posted on Thursday, May 01, 2003 - 3:19 pm: | |
EFWUN asks: "Can you discuss F=MA as F creates increasing velocity as a function of distance and of time?"
Absolutely. Do it all the time. Hell, college students all over the country are doing it right now as we speak.
"You can only evaluate F=MA for one F per equation. Simply, if F varies as a function of increasing rpm, then you cannot evaluate F=MA, other than as a discrete series of instantaneous equations."
You really need to learn freshman calculus... actually, college algebra would work here... you know not what you speak...
You can define F(t) to be any function of time that returns the Force applied to the car, and I can compute a(t) (the acceleration over time) using the formula F(t) = m * a(t)... and I can do that without needing to evaluate more than one equation. I do NOT have to evaluate it for each discrete point in time!! Nor do I need to resort to energy or work equations. This is freshman math for any engineering student.
And I can do it again for F(rpm)... give me the torque curve and I can use F(rpm) = m * a(rpm) to compute very precisely a(rpm)... and I can do that with one equation valuation. For example, let's say you tell me that in first gear "F(rpm) = 2500 - ((rpm - 5000)/100)^2" for 0 <= rpm <= 8500", ignorning units of measure. That corresponds to a torque curve for the car with redline of 8500 rpm and peak torque at 5000rpm. Now, based on that and that 'm = 2500' (again, ignoring units for simplicity), I can compute "a(rpm) = 1 - ((rpm - 5000)/5000)^2" for all values of rpm such that 0 <= rpm <= 8500. Note that the peak value of a(rpm) is at 5000 rpm (peak torque).
We can do the same for functions of t; or, with the addition of one more factoid, we can derive the functions of t from the functions of rpm.
"I thought you wanted to discuss, not harangue me. Read my posts with a little more flexibility in your thinking."
Flexibility? Like being okay with "false = true".
The problem is that you are making blatantly false statements. Other than level of math, its like someone saying "Knowing simply that 'x+y=5' and 'y/x = 1.5', you cannot determine the value of 'x' without considering all discrete values of 'y'." The laws of basic algebra tell me exactly what what 'x' is... and I can determine it with one equation evaluation.
Just because you don't understand how to do math when the variables have functional values (i.e., a function over time), doesn't mean that it cannot be done. What you are saying is simply wrong. No insult intended... it doesn't make you a bad person... but your statements are simply false.
|
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 624
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 3:01 pm: | |
Finally, I viewed the post from the professor at CUNY, and it is quite true, in fact, I derived those equations for Power about 300 posts ago. That site is elementary high-school physics; with all due respect to both the professor and yourself.
I've stated that I will take this up with my old Prof at U Penn, because he is interested and has agreed to give me a couple of hours in his lab, with several of his post-doc fellows. His statement to me was that this is a complex issue, and I believe him.
Your own posts indicate that there is variation unexplainable by simple F=MA. I do not wish to get into another ugly argument; I will close by repeating the equation that makes most sense, is derived from F=MA, and provides the necessary variables to evaluate this conundrum:
F*D=W, and W/time =Power=Delta KE/t, therefore 2Pt=mv final squared - mv initial squared. When we plug in values for those, as I did in my recent posts, we get a rational explanation, which accords with observations, rather than a doctrinal F=MA, which does not accord with observations.
I'm going home to my car and my wife. Please understand that I'm not motivated by the wish to "beat" you, but rather to explain this conundrum to my satisfaction. That ultimate satisfaction will have to wait until a Doctorate from Princeton who is a full Prof of Physics at Penn tells me the definitive answer. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 623
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 2:45 pm: | |
Mr. Alsup, again, you're not taking the time to read a post that disagrees with your own. The equation P=Delta KE/t is true, and is derived from other physical truths, to wit: F=MA, KE=1/2mv squared etc. P=Delta KE/t yields the results I've posted, and they show that "it depends."
Torque by itself accomplishes no work, you must analyze F*D/t to understand this problem. I have posted some very reasonable, logical equations which you yourself have proven correct.
Remember, torque is the measured force on a dyno, but once it accomplishes any rotation, it is work, and that as a function of time is Power.
Again, with all respects to Sir Isaac, calculus is not necessary to derive the equation F*D=W, and W/t =P which equals Delta KE/t. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 622
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 2:38 pm: | |
Mr. Alsup, your post proves the point that it depends. You are assuming certain values for P, but you're not stating the corrolary, to wit; there is a point on the continuum between your example of 268hp, and 380hp where Power curve intersects increasing KE curve, and THAT is the point at which acceleration is maximum.
Similarly, if P was 220hp at P1, and P2 was 405hp, then the car accelerates more quickly right at power peak, illustrating the point, "it depends." |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 599
Registered: 4-2002
| | Posted on Thursday, May 01, 2003 - 2:37 pm: | |
"Can you discuss F=MA as F creates increasing velocity as a function of distance and of time?"
Yes, it is called physics.
"You can only evaluate F=MA for one F per equation."
No, this is the great leap of calculus, invented in 1660 by Newton and Liebeniz (sp). Whti calculus you can use one equation, and evaluate it over all points in time, and integrate to find the solution. Numerical integration is the computers way of performing this kind of math.
"Simply, if F varies as a function of increasing rpm, then you cannot evaluate F=MA, other than as a discrete series of instantaneous equations."
1) it is an 'infinite' serias of instantaneous equations. 'discrete' is used for the numerical methods (i.e. computer) style of integration and differentiation.
2) calculs is the tool that allows you to deal with infinetessimals and integrate them into realistic items.
"Simply put, when F accomplishes ANY forward movement, it becomes F*D or Work. Work as a function of time is Power, and Power = Delta KE/time."
Which physics at CUNY just showed produces an identical solution as f=M*a. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 621
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 2:34 pm: | |
Mr. Alsup, I don't think anyone is ganging up on me. Your posit is perfectly true, but you cannot arrive at a rational conclusion without the necessary variables. Just because P=Delta KE/t and therefore W=1/2MVsquared can be derived from F=MA, does not mean that it doesn't provide the additional variables necessary to the evaluation of an output device accelerating a vehicle of Mass M as a function of increasing velocity and distance over time.
Please remember that the F we are discussing, Torque, does no Work until there is Distance, and in the instant (F not equal to zero and time not equal to zero) that torque creates ANY movement, we have Work/time, or Power. The additional variables and dynamic nature of that equation (which you and I both have proven true) is the proper method to analyze this problem
If we agree that PT equals �mv final squared minus � mv initial squared, then the following values obtain for intervals between 30kph and 35kph, and 50kph and 55kph.
PT=� M (9.72meters/sec)squared -minus- � M (8.33meters/sec) squared (30-35kph)
PT=� M(15.27meters/sec)squared -minus- � M (13.89 meters/sec) squared(50-55kph)
Thus, PT= � M(94.5) minus � M (69.39); and
PT= � M(233.17) minus � M (192.92);
Therefore, assuming M equal to 1;
PT= 12.56 for 30-35kph
PT= 22.125 for 50-55kph.
Let�s make T equal to 1second, and we have
P=12.56 for 30-35kph; and
P= 22.125 for 50-55kph.
Therefore, to create the same acceleration, 5kph/sec squared, we need 22.125/12.56 as our differential P.
Thus differential P2 must be 1.762 times P1. I submit that there are many examples of motors that make twice the power at peak power than they do at peak torque, and therefore, in the speed range demonstrated above, they accelerate faster at peak power than at peak torque. Others do not, and those vehicles will fall somewhere in the range between peak torque and peak power. Finally, some motors fall rapidly off the torque curve as rpm climbs, and these cars will accelerate most rapidly at or near peak torque.
Given that speed ranges, rev ranges, measured torque and calculated power are nearly infinite in variety, I submit that the answer is, �it depends.�
|
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 598
Registered: 4-2002
| | Posted on Thursday, May 01, 2003 - 2:31 pm: | |
"P=12.56 for 30-35kph; and
P= 22.125 for 50-55kph.
Therefore, to create the same acceleration, 5kph/sec squared, we need 22.125/12.56 as our differential P.
Thus differential P2 must be 1.762 times P1"
But we have: P1 = 268 HP, P2 = 380 HP
And: P1/P2 = 1.41, yet we need 1.76 to remain accelerating as fast as we were at '1'. Therefore, acceleration at 50-55 is necessarily less than at 30-35. |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 597
Registered: 4-2002
| | Posted on Thursday, May 01, 2003 - 2:17 pm: | |
Here is a little *.pdf file done by a physics professor at university of brooklyn (CUNY)
http://academic.brooklyn.cuny.edu/physics/tung/course/vg6.pdf
On page 2 it is shown that:
W=F*d
is the same as:
W = 1/2*M*vfinal**2 - 1/2*M*vstart**2
Under the assumption that the vstart = 0, and Mass is constant. Reqwiting 'vfinal' as 'v'
W = 1/2*m*v**2
Which we have shown several times as equivalent and leads to the same conclusion as f=M*a.
Brain: I have not tried to exclude you from this discussion at all, and I am sorry if you have felt this. But since your argument reinforces mine and follows similar thinking patterns, EFWUN might think we are ganging up on him.
|
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 620
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 1:40 pm: | |
Brian, there is a fundamental disconnect in your argument. My point has nothing whatever to do with the engine "spinning itself" or anything else like that. My point is EXACTLY that the engine is an output device, making Torque (Force) times Distance as a function of time, or POWER.
|
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 619
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 1:35 pm: | |
Brian, I can only attempt to get you to understand this, Torque accomplishes NO WORK. You cannot talk about an instantaneous force accomplishing a delta D, rather, once Torque accomplishes the first minute nanosecond of distance, it becomes Work, and Work accomplished within ANY specific interval of time is POWER, or W/T.
Please, let's not let this degenerate into another slanging match, I urge you to consider my statements without rancor. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 618
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 1:32 pm: | |
Brian, I urge you to re-evaluate your statements, particularly the point about my assertion being nonsensical.
Can you discuss F=MA as F creates increasing velocity as a function of distance and of time? You can only evaluate F=MA for one F per equation. Simply, if F varies as a function of increasing rpm, then you cannot evaluate F=MA, other than as a discrete series of instantaneous equations. Simply put, when F accomplishes ANY forward movement, it becomes F*D or Work. Work as a function of time is Power, and Power = Delta KE/time.
I thought you wanted to discuss, not harangue me. Read my posts with a little more flexibility in your thinking.
A car accelerating is not simply instantaneous points on a graph established through calculus, dv/dt as t goes to zero, but rather a system evaluated by the dynamic equation P=Delta KE/t. |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 291
Registered: 3-2002
| | Posted on Thursday, May 01, 2003 - 1:06 pm: | |
EFWUN responds: "I understand what you're saying, I'm saying that dv/dt as t goes to zero yields "instantaneous" A, (the instantaneous slope of the curve at any point) ..."
Okay so far...
"... but I'm saying that is irrelevant to a discussion where distance and time are involved simultaneously."
You cannot have A (acceleration) if distance and time aren't involved. In all cases where A is non-zero, distance is being travelled... except at the instant velocity is zero. Well, I assure you, the fundamental law F=ma applies identically to an object at rest, as an object in motion.
EFWUN continues: "You cannot discuss acceleration of a vehicle due to Force absent rotational distance and the time it takes to accomplish that "Work", unless you're talking about a constant force creating an ever increasing rate of A, or an inelastic collision creating an average A."
A "constant force" will never create "an ever increasing rate of A". F=ma. The only way F can be constant and A increasing is if mass is decreasing. So, ignoring nuclear or relativistic issues, your statement is nonsensical.
You ABSOLUTELY can disuss the acceleration of a vehicle due to a force without bothering with the time and distance required to do the work. The only reason you'd ever bother complicating the math to bring in time/distance/work is if those are in some way affecting F over time. For example, if your engine does not have the energy or power capacity to sustain F over that time or distance. (I gave a practical example of this earlier in the thread... a battery with adequate voltage (force), but not adequate power to drive a high-amperage circuit.) We would need to do a whole lot of ugly math due to this, EXCEPT that it is already done for us! The loss of F or torque due to the engine's power issues are summed up in the engine's torque curve. Even better is the torque curve off the rear wheels which fully includes all the drivetrain effects. Either way, if you use the torque curve as your definition of F, then you can simply compute 'a' (as long as you don't violate the assumptions of the torque curve... exceeding redline, consuming the oxygen supply, dumping all the heat into the air the car is sucking in, etc.).
So, once again, your two basic assertions in this note are plainly false. F=ma is absolutely applicable to a car in motion. Torque from the wheels does not vary due to time or distance... only due to RPM... so as long as we use the torque curve for F, all the power issues are taken care of.
|
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 614
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 12:09 pm: | |
To Repost:
Brian, I understand what you're saying, I'm saying that dv/dt as t goes to zero yields "instantaneous" A, (the instantaneous slope of the curve at any point) but I'm saying that is irrelevant to a discussion where distance and time are involved simultaneously. You cannot discuss acceleration of a vehicle due to Force absent rotational distance and the time it takes to accomplish that "Work", unless you're talking about a constant force creating an ever increasing rate of A, or an inelastic collision creating an average A. Otherwise, W/T equals Power.
Please review the following, and accept my apologies for any inadvertent arithmetic errors, they don't disable the argument.
If we agree that PT equals �mv final squared minus � mv initial squared, then the following values obtain for intervals between 30kph and 35kph, and 50kph and 55kph.
PT=� M (9.72meters/sec)squared -minus- � M (8.33meters/sec) squared (30-35kph)
PT=� M(15.27meters/sec)squared -minus- � M (13.89 meters/sec) squared(50-55kph)
Thus, PT= � M(94.5) minus � M (69.39); and
PT= � M(233.17) minus � M (192.92);
Therefore, assuming M equal to 1;
PT= 12.56 for 30-35kph
PT= 22.125 for 50-55kph.
Let�s make T equal to 1second, and we have
P=12.56 for 30-35kph; and
P= 22.125 for 50-55kph.
Therefore, to create the same acceleration, 5kph/sec squared, we need 22.125/12.56 as our differential P.
Thus differential P2 must be 1.762 times P1. I submit that there are many examples of motors that make twice the power at peak power than they do at peak torque, and therefore, in the speed range demonstrated above, they accelerate faster at peak power than at peak torque. Others do not, and those vehicles will fall somewhere in the range between peak torque and peak power. Finally, some motors fall rapidly off the torque curve as rpm climbs, and these cars will accelerate most rapidly at or near peak torque.
Given that speed ranges, rev ranges, measured torque and calculated power are nearly infinite in variety, I submit that the answer is, �it depends.�
More to come!
|
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 613
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 12:07 pm: | |
Brian, you're ABSOLUTELY welcome to discuss anything with me, ANYTIME! I actually responded to your post above. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 612
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 12:06 pm: | |
Rich, you're right, because the truth is that my post is derived purely from physics. There are scientific absolutes, and situations where science tells us that we must evaluate the variables to arrive at a case-specific determination.
Remember, P=Delta KE/time is derived from F=MA, and D=1/2ATsquared etc. It is not outside the realm of newtonian physics, but rather squarely within that realm, and therefore absolutely true. What it says is that a certain amount of power will create a certain change in the velocity of a given mass over time. The analysis includes the fact that KE is increasing as a square of velocity, and therefore, depending on speed range, and power output, "it depends!"
The inquiry has nothing whatever to do with the "energy?" expended to turn the crank, this is a simple question of output, frictional losses have nothing to do with it. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 611
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 12:00 pm: | |
The inquiry has nothing whatever to do with "frictional losses" or the energy of spinning the crank! We're talking about an output device, pure and simple. Torque*Distance over time has nothing to do with spinning the crank, but rather moving the vehicle forward and accelerating it. |
rich (Dino2400)
Junior Member
Username: Dino2400
Post Number: 204
Registered: 10-2001
| | Posted on Thursday, May 01, 2003 - 11:59 am: | |
"Given that speed ranges, rev ranges, measured torque and calculated power are nearly infinite in variety, I submit that the answer is, �it depends.�
----
To me, this is just a much more attractive statement than anything else we've heard from anyone in this thread. But I know that the scientist types, who feel a need for absolutes in their life, would still much prefer the one simple rule that will describe all cases. Of course the history of science is simply the history of previous simple "facts" being overturned by new ones, but that doesn't seem to bother them for some reason, ha! |
Faisal Khan (Tvrfreak)
Junior Member
Username: Tvrfreak
Post Number: 71
Registered: 3-2003
| | Posted on Thursday, May 01, 2003 - 11:44 am: | |
If there are any frictional losses, then they affect the amount of torque getting through to the wheels linearly. Which means that the car's peak acceleration still happens at peak torque, no matter how much is consumed by other components such as the crankshaft.
If this internal loss (consumption of torque) varies non-linearly, then peak torque will not produce peak acceleration for the car. Otherwise it will. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 610
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 11:42 am: | |
Brian, I understand what you're saying, I'm saying that dv/dt as t goes to zero yields "instantaneous" A, (the instantaneous slope of the curve at any point) but I'm saying that is irrelevant to a discussion where distance and time are involved simultaneously. You cannot discuss acceleration of a vehicle due to Force absent rotational distance and the time it takes to accomplish that "Work", unless you're talking about a constant force creating an ever increasing rate of A, or an inelastic collision creating an average A. Otherwise, W/T equals Power.
Please review the following, and accept my apologies for any inadvertent arithmetic errors, they don't disable the argument.
If we agree that PT equals �mv final squared minus � mv initial squared, then the following values obtain for intervals between 30kph and 35kph, and 50kph and 55kph.
PT=� M (9.72meters/sec)squared -minus- � M (8.33meters/sec) squared (30-35kph)
PT=� M(15.27meters/sec)squared -minus- � M (13.89 meters/sec) squared(50-55kph)
Thus, PT= � M(94.5) minus � M (69.39); and
PT= � M(233.17) minus � M (192.92);
Therefore, assuming M equal to 1;
PT= 12.56 for 30-35kph
PT= 22.125 for 50-55kph.
Let�s make T equal to 1second, and we have
P=12.56 for 30-35kph; and
P= 22.125 for 50-55kph.
Therefore, to create the same acceleration, 5kph/sec squared, we need 22.125/12.56 as our differential P.
Thus differential P2 must be 1.762 times P1. I submit that there are many examples of motors that make twice the power at peak power than they do at peak torque, and therefore, in the speed range demonstrated above, they accelerate faster at peak power than at peak torque. Others do not, and those vehicles will fall somewhere in the range between peak torque and peak power. Finally, some motors fall rapidly off the torque curve as rpm climbs, and these cars will accelerate most rapidly at or near peak torque.
Given that speed ranges, rev ranges, measured torque and calculated power are nearly infinite in variety, I submit that the answer is, �it depends.�
More to come!
|
rich (Dino2400)
Junior Member
Username: Dino2400
Post Number: 203
Registered: 10-2001
| | Posted on Thursday, May 01, 2003 - 11:38 am: | |
what's "not true"? That torque peak at output shaft is most likely very similar to torque peak at the wheels? |
Faisal Khan (Tvrfreak)
Junior Member
Username: Tvrfreak
Post Number: 69
Registered: 3-2003
| | Posted on Thursday, May 01, 2003 - 11:27 am: | |
Not true, unless the percentage losses vary non-linearly with rpm. |
rich (Dino2400)
Junior Member
Username: Dino2400
Post Number: 202
Registered: 10-2001
| | Posted on Thursday, May 01, 2003 - 11:20 am: | |
But Brian, one assumes that torque peak figures quoted by manufacturers are taken from the engine only, i.e. at the output shaft. I suppose it is possible that an owner may test his car on the dyno and find that actual torque peak at the wheels is different than at the output shaft because of the things you mentioned. But I suspect that it will be at very similar rpm to the output shaft torque peak. |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 288
Registered: 3-2002
| | Posted on Thursday, May 01, 2003 - 10:32 am: | |
It appears I am not really welcome in this discussion... EFWUN and Alsup seem to only want to talk to each other... or should I say, about each other... but I have to respond to EFWUN's recent post:
EFWUN says: "My point, distilled, is that F=MA (while absolutely the basis of Newtonian Physics), does not properly evaluate the system where F is neither instantaneous nor absolutely constant."
Absolutely false. F=ma is just universally true. Vary F any way you please and the 'a' caused by that can be computed with that formula... and vice-versa. The math gets more complicated, that is all. Any other assertion is just silly... this is a fundamental law, and one of the best known laws of physics, at that. Your continued insistence otherwise, combined with your past insistence that differential calculus doesn't work, really undermines anything else you are arguing.
Then EFWUN states: "Torque (Force) times Distance (rotation of the output shaft) equals Work, the ability to impart energy to a system [...]"
Not false, but irrelevant to the problem we should be discussing. The issue is NOT how much work the engine is doing to spin itself... that's only an issue if we are focusing on building a more energy efficient engine. The issue in this discussion is how much work the engine is doing to move the car forward... to accelerate the car.
You may want to argue its the same difference since its mechanically connected to the wheels... however, its not the same difference, because you have continuously in this discussion confused yourself by making that simplification... you forget the gearing in between or you make arguments for the cases when they aren't connected. Note that accelerating the crankshaft and accelerating the car are two different things, though they are related. Some energy is spent accelerating the drive train; some energy is spent accelerating the car. The amount of forced required to accelerate the drive train reduces the amount of force actually applied to the car. In most situations, we don't care about the energy and force required to accelerate the spinning of the crankshaft and drivetrain... we factor that out... we just focus on accelerating the car. I suggest you do the same... focus on the car... because the more complex computations required to factor in the drivetrain are leading you awry.
|
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 595
Registered: 4-2002
| | Posted on Thursday, May 01, 2003 - 10:25 am: | |
"Mr. Alsup's post now indicates that peak acceleration occurs "within spitting distance" of torque peak, not AT torque peak."
Previously, we had been using the caveat of 'no air resistance'. With no air resistance max acceleration still occurs at peak TQ.
Then we find that when we add realistic air resistance, that peak acceleration stays at peak TQ (within spitting distance).
When we find that; for the first 5 gears max acceleration occurs at peak TQ (with or without air resistance) and that (with the TQ curve as used) max acceleration in 6th gear occurs at 1000 RPMs! Just about as far from peak HP as one can get!
"Simply stated, that interaction is "at what point on an ascending graph of engine revolutions does the Delta KE of the vehicle (and aero drag, also increasing as a square function of velocity) increase so dramatically that 2*P*T at Peak Power accomplishes less Delta Velocity (acceleration) than 2*P*T at some other rev point? E.g., somewhere between torque peak and Power peak. "
We went through the delta KE evaluation and showed that the power required to gain 1 MPH increases linearly as speed increases. By dividing the power available by the power required we arrive at a metric of time to gain a unit of velocity. Then we found that a) the shape of this curve 'looks' just like the shape of the TQ curve, and b) delta KE leads to the same conclusion as f=M*a.
And as shown, it occurs BELOW peak TQ not between peak TQ and peak HP. And the amount below peak TQ is almost immesurable (1st through 5th).
"Torque (Force) times Distance (rotation of the output shaft) equals Work, the ability to impart energy to a system, and that ability as a function of time F*D/T equals Power, is a valid analysis of what occurs as a vehicle of Mass M accelerates across distance and time."
And, likewise, we showed that W=f*d leads to the same conclusion as delta KE and f=M*a. Then we went on to show that even in the presence of air resistance, the simplified results are 'perfectly' accurate for the first 4 gears and 'colloquially' accurate for 5th gear.
"This is the natural extension of these analyses, and the mere fact that Mr. Alsup has shown that peak acceleration isn't occuring EXACTLY at peak torque indicates the need for further, more complex evaluation."
But you will have to admit that peak acceleration occurs so close to peak TQ that the typical reader SHOULD walk away from this conversation with the "simplified" notion that peak acceleration occurs AT peak TQ. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 607
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 9:45 am: | |
To quote Mr. Alsup: "Nobody is saying that an engine does not produce more power at higher RPMs. We are saying that it takes correspondingly MORE power to gain a single MPH at 50 MPH than at 30 MPH. The increase in power required is greater than the increase in power available, and thereby, acceleration goes down!"
This is a clear indication of my thesis. At what point (and we must admit there are some) will 2*P*T at peak power admit of a greater delta Velocity than at some point lower on the rev and velocity graph? We cannot assume arbitrary values of say 50kph or 100kph. I will sort out the actual values, but I'm too busy today.
Thanks for the interest. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 606
Registered: 2-2003
| | Posted on Thursday, May 01, 2003 - 9:37 am: | |
Mr. Alsup's post now indicates that peak acceleration occurs "within spitting distance" of torque peak, not AT torque peak.
I concur that KE increasing as the square of velocity, rather than on a linear basis, changes the evaluation somewhat as well.
Nevertheless, remember that units of Power are large (e.g., HP is a concentration of those units, don't remember exactly but 550lb-ft/sec sounds right), and 2PT=M(delta Vsquared) clearly indicates the relationship between Power, Time and Acceleration.
As KE increases as the square of velocity, will we find that there are points where KE has increased so much that 2PT at that point accomplishes less delta Velocity than at some point lower down the velocity range? Yes. Does this indicate that "it depends" is the answer? Yes.
These are not absolutist posts; I believe, however, that the evaluation is complex, and I hope to have further elucidation soon. Similarly, I know that BMEP is torque.
My point, distilled, is that F=MA (while absolutely the basis of Newtonian Physics), does not properly evaluate the system where F is neither instantaneous nor absolutely constant. Rather, the derivation:
Torque (Force) times Distance (rotation of the output shaft) equals Work, the ability to impart energy to a system, and that ability as a function of time F*D/T equals Power, is a valid analysis of what occurs as a vehicle of Mass M accelerates across distance and time.
The very fact that Mr. Alsup has now posted acceleration occuring "within spitting" distance of torque peak is indication that a more complex interaction is occuring.
Simply stated, that interaction is "at what point on an ascending graph of engine revolutions does the Delta KE of the vehicle (and aero drag, also increasing as a square function of velocity) increase so dramatically that 2*P*T at Peak Power accomplishes less Delta Velocity (acceleration) than 2*P*T at some other rev point? E.g., somewhere between torque peak and Power peak.
This is the natural extension of these analyses, and the mere fact that Mr. Alsup has shown that peak acceleration isn't occuring EXACTLY at peak torque indicates the need for further, more complex evaluation.
Values to follow in a day or so. |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 519
Registered: 6-2002
| | Posted on Monday, April 28, 2003 - 11:58 pm: | |
Brian - our thoughts have converged. I agree with everything you have posted subsequent to my post.
--------------------------------------------------
Mitch - "So when one considers W=f*d in imparting energy into the car, the 'd' must represent the distance that 'that unit' of work applied to the car, and not the other distance that the car travels based on its current velocity (v*t)."
--------------------------------------------------
As Brian has observed, it is critical that we choose the appropriate frame of reference, which in this case is a black box engine and a car. Work performed is force x distance that car travels, not the internals of the black box. Once the car achieves a given momentum (mass x velocity), it will maintain that momentum forever (unless acted upon by an outside force - e.g. friction and wind resistance). In the ideal of no friction, the car continues on in the same direction forever, yet no additional work has been performed (as Brian correctly observed - force equals zero). The initial work raised the car's kinetic energy (1/2 x mass x square of velocity).
In fact, work always changes the energy of a system, either kinetic or potential. Work that raises the height of the car imparts potential energy, while work that accelerates the car contributes kinetic energy.
We're back to basic physics here, but I believe this is important, as Tim suggested in an earlier post. Most important is to set-up the problem, and isolate the forces and objects being influenced.
Jim S. |
Frederick Thomas (Fred)
Member
Username: Fred
Post Number: 699
Registered: 2-2001
| | Posted on Monday, April 28, 2003 - 11:56 pm: | |
Rob,
Didn't one get to around 500. Maybe the world trade center subject? |
PSk (Psk)
Member
Username: Psk
Post Number: 395
Registered: 11-2002
| | Posted on Monday, April 28, 2003 - 11:52 pm: | |
Mitch,
100% agree with your comment regarding why power is hunted in motor racing. After all torque is just a function or cc size and combustion efficiency thus in a professional series this should be fairly even. Thus if you can rev that little bit more you have that little bit more torque multiplication advantage for that little tiny bit more that you can hold that gear ... or maybe even change to a even better ratio.
Thus we have ended up back where we were many days/weeks ago:
Torque is for acceleration and Power is a measurement of how much torque you can produce per rpm ... thus how well your engine is able to continue to make torque the higher you rev it ... useful for high speed.
Pete |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 587
Registered: 4-2002
| | Posted on Monday, April 28, 2003 - 11:23 pm: | |
"Why does this work on the race track to result in maximum performance?"
My opinion:
When a formula (set of specifications for racing) fixes the maximum size of an engine;
a) everybody gets pretty much the same gasoline, and this sets a limit to the compression ratio.
b) everybody uses the maximum allowed displacement.
c) everyone gets rid of as much friction as possible
d) everyone gets rid of as much rotating and reciprocation weight as possible.
Therefore, to first order, everybody can get to about the same max TQ somewhere in the RPM band.
e) HP = TQ*RPM/5252, so if you can move the torque curve up the RPM band, you will get more power. Power sets max speed, and power allows one to use TQ multiplication through gears to achieve more thrust. |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 586
Registered: 4-2002
| | Posted on Monday, April 28, 2003 - 11:11 pm: | |
I thought it might be fun to see what happens when air resistance is included in the computations. The first graph shows the original horsepower graph drawn with relation to the speed of the vehicle. To this I have added a term that represents the amount of power it takes to push a F355 through the air, and subtracted this term from each HP[gear] (shown in dotted form)
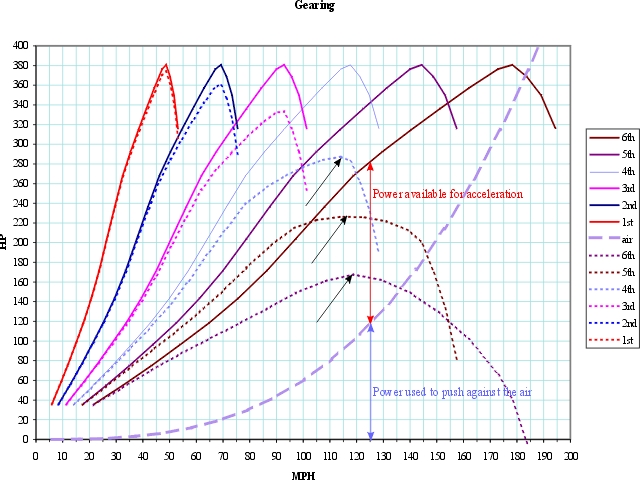
I arbitrarily set the air resistance power to consume all available engine power at 183 MPH (rated top speed) of the F355. As drawn this intersects above peak HP. Perhaps the engine revs out to here, or perhaps tire growth makes the difference. In any event, I used the data as drawn.
Notice the velocity around 117 MPH, this is the point where maximum power is available for acceleration in 4th, 5th and 6th gears! Notice that the power available for acceleration above 120 MPH continually declines!
The second chart simply converts HP back into TQ using our definition tq=hp*RPM/5252.
Notice that the point of maximum acceleration (if you believe my side of this argument) in the first 5 gears is within spitting distance of peak TQ. In 5th gear there are 3MPH difference, in 4th less than 1 MPH from peak TQ. |
PSk (Psk)
Member
Username: Psk
Post Number: 393
Registered: 11-2002
| | Posted on Monday, April 28, 2003 - 7:15 pm: | |
Brian,
You have hit the nail on the head and proved why W=F*D, as as you pointed out the distance travelled is irrelevant.
To step back for a minute, I think you misunderstood Mitch's post and his comments also proved that D is irrelevant which means we are back to F being what Acceleration is all about.
Work no matter how you slice it involves time or distance. Acceleration does not it is the rate of change of velocity ... thus F=m.a is all we need and the body (car) will accelerate the most when the force applied to it (once all opposing forces have been deducted) are at a maximum.
Where does this force come from?
It comes from our engine ... but has nothing to do with work that it can get done, because we are not interested in how far we can travel, etc.
Thus work out what produces the maximum force at the rear wheels and you have peek acceleration in that gear for those ratios and conditions, etc.
Regarding race prepared Ford BDA engines that EFWUN has raced. My engine builder used to build those and they used to rev to something like 105000 rpm and had NO torque, thus they were all revs and nothing else. Why does this work on the race track to result in maximum performance? Simply due to gear ratio mechanical advantage (as we have already discussed). Thus for the race track and a vehicle with gear ratios involved, maxing your rev's is the way to go as this means you can INCREASE your mechanical advantage through your gear box by increasing you ratios.
Thus a car that revs to 5000rpm and one that revs to 10000rpm, for the same speed per gear the 10000rpm car can run a 2x higher ratio thus meaning that whatever torque that engines produces is being multiplied by 2x more than the OTHER engine. Thus the low torque racing engine COULD end up with more rear wheel torque than the 5000rpm engine, and thus accelerate faster!
Pete |
Rob Lay (Rob328gts)
Board Administrator
Username: Rob328gts
Post Number: 4635
Registered: 12-2000
| | Posted on Monday, April 28, 2003 - 3:42 pm: | |
I think this is officially the largest thread in FerrariChat.com history and it actually has somewhat to do with Ferraris! |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 281
Registered: 3-2002
| | Posted on Monday, April 28, 2003 - 2:53 pm: | |
"On each power stroke, the car absorbs energy and goes faster*. However the work imparted to the car remains fixed to the 'd' distance that the piston moves, not the distance 'd' that the car moves! In fact, after 'getting to speed', one can turn the engine off, and continue to gain distance (V>=0). Clearly no work is being performed, yet distance continues to accumulate."
No work is being performed because F has gone to zero, not D! If we are talking about the car's ability to accelerate, the D the piston travels is not relevant, UNLESS you are also going to do all the computations around the significant energy losses in the engine and drivetrain. The work being done to move the pistons is the work that must be INVESTED/CONSUMED in the effort to convert the energy trapped in the fuel into kinetic energy that can be applied to the car. Relative to torque and horsepower curves, that is all factored out...
In setting up these problems, you need to focus on the car and leave the engine as a black box... or you will get to dissertation-length physics to desribe what's going on.
|
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 585
Registered: 4-2002
| | Posted on Monday, April 28, 2003 - 2:36 pm: | |
"A motor turns heat into Power,"
Yes
"with a calculable rate of efficiency."
As long as the efficiency can change with RPMs, still OK.
"If we evaluate thermodynamics, there are twice as many explosions (heat events) at 8,000rpm as at 4,000rpm. While those heat events at 8k might not be as optimally efficient as the heat events at 4,000rpm (cylinder filling and exhaust scavenging), they nevertheless result in FAR more fuel being burned, and FAR more Brake Mean Effective Pressure per unit time."
By the way, BMEP is Torque, not HorsePower. And while we are here, everyone should note that the engine is most efficient at converting a mixture of gasoline and air into (TQ and/or HP) at peak TQ than at any other point of operation.
"Simply put, our output device (the motor) makes nearly twice the power because it is burning nearly twice the fuel at 8k, and twice the power can accomplish nearly twice the work over any given interval of time. Can we ignore this evidence of another contributing factor to acceleration? NO."
Nobody is saying that an engine does not produce more power at higher RPMs. We are saying that it takes correspondingly MORE power to gain a single MPH at 50 MPH than at 30 MPH. The increase in power required is greater than the increase in power available, and thereby, acceleration goes down! |
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 584
Registered: 4-2002
| | Posted on Monday, April 28, 2003 - 2:26 pm: | |
There is an interesting issue with respect to the W=f*d equation. Consider a single cylinder engine performing work pushing a car forward. Arrange this engine so that the work is extracted while the piston moves forward with the car (power stroke pushes piston forward--in the same direction car travels).
On each power stroke, the car absorbs energy and goes faster*. However the work imparted to the car remains fixed to the 'd' distance that the piston moves, not the distance 'd' that the car moves! In fact, after 'getting to speed', one can turn the engine off, and continue to gain distance (V>=0). Clearly no work is being performed, yet distance continues to accumulate.
So when one considers W=f*d in imparting energy into the car, the 'd' must represent the distance that 'that unit' of work applied to the car, and not the other distance that the car travels based on its current velocity (v*t).
* at least until the power required to hold the car at speed equals the power available to accelerate the car to a faster speed. |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 278
Registered: 3-2002
| | Posted on Monday, April 28, 2003 - 1:22 pm: | |
Valid point, James... heat generation is fundamental to a combustion engine. However, in an idealistic engine, *all* the heat generated would be converted into kinetic energy, rather than "wastefully" removed by oil and water coolers. That is, taking the engine as a black box, a tremendous amount of energy goes in (in the form of fuel), some is delivered to the wheels, some radiated off as unused heat, and some expelled in the exhaust (some as unburnt fuel).
Anyway, my real point is that in applying the "energy equations" and "work equations", you need to make sure you are looking only at the work done by the car as a whole... in other words, F is the force pushing the car forward and D is the distance travelled by the car. Looking at internal characteristics (like the D travelled by the crankshaft) will cause you to come up with very different answers... because you'll be looking at all that energy that is inefficiently NOT delivered to the wheels.
My goal was to try to explain how EFWUN might be correctly computing the equations, but solving a different physics problem. (In my experience, the hard part of physics is setting up the problem properly, not performing the math.)
FWIW. |
Faisal Khan (Tvrfreak)
New member
Username: Tvrfreak
Post Number: 28
Registered: 3-2003
| | Posted on Monday, April 28, 2003 - 12:57 pm: | |
EFWUN,
delta means change. Change is measured over unit increments. To get increasingly accurate measurements of this change, you sum up the change in values (deltas) over each of these increments, while making the increments increasingly smaller. As the increments approach zero, you do get instantaneous points of force or torque.
There is no difference between analyzing it by equations or by doctrine, unless the doctrine contradicts the equation premises. In this case, the doctrine is not in contradiction, there is no conundrum, and the interplay of equations here don't defy easy, doctrinaire evaluation. It's a simple model. The world is complex. The more factors (or complexity) you introduce, the more the model has to take those into account. But the underlying physics do not change.
This is beyond trivial for any potential Nobel laureate. Definitely a case of beating a dead cavallino.
Best,
Faisal. |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 518
Registered: 6-2002
| | Posted on Monday, April 28, 2003 - 12:37 pm: | |
Brian - I believe that your response has helped to clarify and support the "curiosity" of your initial post.
--------------------------------------------------
"James, Its not clear to me what you're saying I got wrong or what I said that was illogical. Its also unclear to me what point you were making. Take any engine, dump its engine oil, and instantly the engine will start producing more heat and yielding less net power to the wheels. An engine really isn't a heat pump... it is converting the energy stored in fossil fuels into kinetic energy... and some heat, which is just an incidental (waste) output."
--------------------------------------------------
The heat generated by an engine is not merely a consequence of internal friction, but a fundamental requisite. Fossil fuel is burned to create heat, which rapidly increases the pressure (not really an explosion) of the gas contained in the cylinder. This pressure against the surface area of the piston does work. Thus, the engine acts as a device to convert heat into mechanical work.
In fact (as I discussed previously), attempts to have engines run cooler (bigger fans, radiators, chemicals in the coolant, etc.) act contrary to the thermodynamic process. IN THE LIMIT, if one were to cool the engine block to ambient temperature, then the combustion of fuel would create heat that did nothing but warm the air around the engine. There would be no heat to increase the pressure of the contained gas. Heat would be flowing across the cylinder wall to the coolant, removed to the atmosphere, and not available to do work.
Internal friction creates heat, but is minor and of little consequence to this process. The rapid expansion of gas in the cylinder is approximately adiabatic in nature, that is, without loss of heat. Thus, the pressure is constant as the volume of the cylinder increases (with piston displacement). The heat necessary to maintain adiabatic expansion comes from the cylinder wall, otherwise the contained gas would cool as the piston moved, reducing the force against its crown.
FINALLY, the ONLY way to create more heat, and thus to do more work, is to pump more fuel for combustion into the cylinders per unit time. This is accomplished through higher RPM. (Assuming constrained displacement - 3 liters for example. Also assuming normal aspiration or forced induction - turbocharged, either one, doesn't matter). Think of the engine as a black box - the more heat it can create, the more work it can do. Notice that I did not say the higher the temperature, as it is designed to convert heat into mechanical work, without raising the temperature above a designed limit (the real truth around adiabatic expansion).
Again, we are likely saying the same thing, but I believe that heat is an essential element of the process, not a consequence.
Jim S. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 605
Registered: 2-2003
| | Posted on Monday, April 28, 2003 - 11:27 am: | |
Well, Faisal, his comments did get my "hackles" up!! There is no reason, however, to ignore the inquiry into Delta Kinetic Energy, because it explains Power, rather than relying on instantaneous points of Force, or torque.
There is an interplay of equations here that defy easy, doctrinaire evaluation.
The physics prof to whom I refer indicated that there is more to the evaluation than either simple torque, or simple power, and indicated an interest in evaluating this problem. That, for me, indicates that there IS a conundrum, as does Mr. Alsup's own statement, "torque creates low velocity acceleration, while Power overcomes increasing wind resistance."
|
Faisal Khan (Tvrfreak)
New member
Username: Tvrfreak
Post Number: 27
Registered: 3-2003
| | Posted on Monday, April 28, 2003 - 11:21 am: | |
EFWUN,
there is NO "conundrum." It is a closed system of physical equations that are being used to describe physical phenomena. All of them agree with everything Mitch says. They all concur and yield the same results. Other variables might influence these results but they don't change the underlying physics involved.
Due to his over-reliance on differentiation and integration, and his abominable spelling and grammar, Mitch made his point in a very complex manner. Todd did an awesome job of putting it in layman's terms.
I think Mitch's rudeness has gotten your hackles up, and now you are stubbornly refusing to admit the validity of his points.
Rgds,
Faisal. |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 602
Registered: 2-2003
| | Posted on Monday, April 28, 2003 - 11:09 am: | |
Further, Dr. Selevan has again tickled us with another means of inquiry into this problem, thermodynamics.
Simply, a motor converts fuel and air into heat. In analyzing fuel mileage, I can state that in my youth, the means of stretching fuel mileage in our Can Am racer was simply to SHORT SHIFT, e.g., 7,500rpm instead of 8,500rpm. Trap speeds went down, lap times went up, and hopefully, you made it to your pit stop because you were BURNING LESS FUEL.
Importance for this discussion? A motor turns heat into Power, with a calculable rate of efficiency. If we evaluate thermodynamics, there are twice as many explosions (heat events) at 8,000rpm as at 4,000rpm. While those heat events at 8k might not be as optimally efficient as the heat events at 4,000rpm (cylinder filling and exhaust scavenging), they nevertheless result in FAR more fuel being burned, and FAR more Brake Mean Effective Pressure per unit time. Simply put, our output device (the motor) makes nearly twice the power because it is burning nearly twice the fuel at 8k, and twice the power can accomplish nearly twice the work over any given interval of time. Can we ignore this evidence of another contributing factor to acceleration? NO.
Finally, arbitrarily assigning values to KE and therefore restraining the inquiry into Power is intellectually dishonest. Power must be evaluated by the simple output of the motor, rather than by any mathematical sleight of hand from the opposite side of an equation with variables. Remember, WE assign the value to Power, it is not assigned from mathematical manipulation of E (what I'm calling Kinetic Energy) |
EFWUN (Efwun)
Member
Username: Efwun
Post Number: 601
Registered: 2-2003
| | Posted on Monday, April 28, 2003 - 10:56 am: | |
Hi, guys! No, Mr. Alsup has not "chased me away", but I have determined not to pursue this thread on a daily basis as a way of keeping my blood pressure (and blood lust!!) down!
I understand that dv/dt as t goes to Zero is the instantaneous slope of a graph equal to A. What I am saying is that an evaluation that recognizes additional variables yields a different conclusion. That equation is P=W/t = Delta KE/t. Remember that Kinetic Energy is just 1/2MVsquared, and delta KE is a function of delta V as a function of time, or A.
F=MA is by definition, truth, however, it does not explain F or A as a function of change in velocity or time. Over any discrete rational interval of time, F*D=W, and W/T equals Power, and Power = Delta KE over time. Therefore, this is an equation that explains at least a portion of this conundrum.
Simply put, if we consider the motor as an output device, a motor with 300 units of torque at 4,000rpm and 250 units of torque at 8,000rpm is putting out nearly twice the Work per unit time at 8,000rpm than at 4,000rpm. This has application as our vehicle gains velocity as a function of time and distance.
Mr. Alsup has stated that torque results in low velocity acceleration, while power is necessary to overcome increasing wind resistance. Is this not an admission that there are more variables to this problem than simply "instantaneous" torque equaling mass times acceleration?
I have previously stated that torque is a motor's ability to overcome static resistance, e.g., strain against the "brake" of a dyno, or yank out a tree stump etc. Work is the result of that torque as ANY distance whatsoever is travelled, and Power is the result of that Work as ANY time whatsoever has passed.
Clearly, a vehicle accelerating across distance and time (has a kinda Star Trek ring to it, no?) is not an instantaneous point on a graph, but rather an entity where work accomplished as a function of time results in increasing velocity.
Again, one cannot, as Mr. Alsup has, insist that F=MA is the only inquiry in acceleration OF A REAL VEHICLE, NOT ON A BLACKBOARD, and yet state that torque is responsible for low velocity acceleration and power is responsible for overcoming wind resistance. That statement demonstrates that there more issues here than meet the doctrinal eye, (by doctrinal I mean adherence to doctrine and an inherent disregard for intellectual inquiry and discussion).
A gentleman who may well wind up nominated for a Nobel has indicated a curiousity about this subject, and invited me to join him for an afternoon's discussion of these issues at Penn in a couple of weeks. This is an honor I'm loathe to forego, particularly given the heated nature of this thread.
I think that, other than pop on here briefly to prevent this from being a filibuster by a gentleman (Mr. Alsup) who violently disagrees with my inquiry, I will wait for further elucidation from the physics professor I referenced above.
|
Mitch Alsup (Mitch_alsup)
Member
Username: Mitch_alsup
Post Number: 582
Registered: 4-2002
| | Posted on Monday, April 28, 2003 - 10:27 am: | |
By using:
E=1/2*m*v**2
dE/dt = m*v*a = P
So in the range of maximum power: P is (relative) constant.
Then:
P = K1 = K2*v*a
Or
a = K3/v
So: at the point of maximum power, acceleration has already headed downward, and therefore acceleration cannot be at its maximum when the engine power is at its maximum.
A similar argument holds for work. It takes more work to accelerate from 50 to 51 MPH than it takes to accelerate fvrom 30 to 31 MPH. In the W=f*d equation this is represented by the increase in distance traveled while acceleration from 50 to 51 than the distance traveled while accelerating from 30 to 31. The distance traveled per unit time is simply v*t; so unless power is also increaseing at the same rate, acceleration slows down. The point at which power is increaseing at a linear rate is (you guessed it) peak TQ. |
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 273
Registered: 3-2002
| | Posted on Sunday, April 27, 2003 - 9:59 pm: | |
James, Its not clear to me what you're saying I got wrong or what I said that was illogical. Its also unclear to me what point you were making. Take any engine, dump its engine oil, and instantly the engine will start producing more heat and yielding less net power to the wheels. An engine really isn't a heat pump... it is converting the energy stored in fossil fuels into kinetic energy... and some heat, which is just an incidental (waste) output. |
James Selevan (Jselevan)
Member
Username: Jselevan
Post Number: 516
Registered: 6-2002
| | Posted on Sunday, April 27, 2003 - 7:21 pm: | |
Brian K. - Nice dessertation, although I believe part of your logic is a bit illogical.
--------------------------------------------------
"THUS, although both engines have NET power the same... one engine is actually producing more energy and power, but that excess power and energy is being consumed by the engine itself... just moving those parts... and in all likelihood, generating much more heat. An F1 engine will be like this... it gets an amazing amount of NET power out of a 3L engine... but it does so by making it spin really fast... that causes it to have to move those internal parts really fast... which means it has to generate a lot of power just to accelerate its own internal parts... and it produces a tremendous amount of heat (which is energy it produces, but just gets wasted... it doesn't help do the work its really trying to do... accelerate the car). Now the F1 engine engineers know all this, so they are trying to minimize the amount of work that gets wasted just moving the engine internal parts. They do that by minimizing the mass of those moving parts and by minimizing the internal friction."
--------------------------------------------------
As discussed below, the internal combustion engine is nothing but a heat pump. It converts heat into mechanical work. The more heat it can generate - the more work it can do. Thus, given a constrained displacement - how does one get more air:fuel mixture through the pump in a given amount of time? - By increasing throughput with filling and emptying cylinders as fast as possible - read RPM.
Give me more RPM and I can give you more combustion in the any given time interval. This means rapidly reciprocating masses - the scorn of internal combustion engines. Thus, to facilitate high RPM, one lightens materials (multivalve - for example).
Internal friction losses and heat generated by friction are consequences of the process - not a justification for producing more power as your post suggests. (I read a slight twist in your logic - perhaps we are saying the same thing).
Jim S. |
Todd Wasson (Todd_wasson)
New member
Username: Todd_wasson
Post Number: 8
Registered: 4-2003
| | Posted on Saturday, April 26, 2003 - 7:21 pm: | |
Rich,
From what I see, this only proves that there is more power at the higher rpm (and a faster rate of change of kinetic energy). If we changed Efwun's example to have a flat torque curve with 300 work units at both speeds, all that happens is power doubles when rpm doubles. According to f=ma, the acceleration remains the same.
His argument is surrounding the rate of change of kinetic energy, and I don't understand what he's getting at there or why it would change anything. I'll have to go through his posts from earlier on and see if I can pick up on it.
|
Brian Kennedy (Kennedy)
Member
Username: Kennedy
Post Number: 269
Registered: 3-2002
| | Posted on Saturday, April 26, 2003 - 6:52 pm: | |
Wait! I think I finally understand EFWUN's position! Not sure EFWUN is still listening to validate, but one of his last few posts keyed me into the following interpretation and correction:
EFWUN said, "Power equals work/time, which equals work*distance/time. Work equals force times distance, correct? So, if at 4,000rpm,Force is equal to a value of 300, and distance (say the rotation of the crankshaft) is equal to a value of 1, then we have W=300, right? If at 8,000rpm force is equal to 250, and distance (two rotations of the crankshaft) is equal to 2, then W=500, right? Okay, so, now, let's say time equals 1 (just so we don't have any of that pesky calculus). W/t equals power, right, so let's see, Power at 4,000rpm equals 300units, while Power at 8,000rpm equals 500units. "
EFWUN is looking at force being produced by the engine AND the distance being travelled by the crankshaft rotation... from that he is computing the energy and power numbers.
There is a fundamental error there in the problem setup. Think of the car engine and drive train as a black box. You don't know if its spinning or what on the inside... you don't know about a crankshaft or gears or otherwise... it just somehow accelerates the car. Now if you want to measure the work the engine is doing, you'd measure what? The force it applies to the car and the distance the car travels. Let me emphasize that: the distance the car travels.
Now let's white box the engine just a bit... we find two engines that produce exactly the same amount of acceleration to the exactly same car. They are doing the same work, and producing the same power. But then we are told that the internal parts in one are moving twice the distance as the internal parts of the other engine. Does that suddenly change our calculation of how much power the engine is producing???
Yes and no. Considered as a black box, NO... it doesn't matter how each engine does its job... they are doing the exact same job. However, what it does change is our calculation of how much energy the engine parts themselves are consuming... how much energy the engine must produce to overcome its own internal friction and inertia.
THUS, although both engines have NET power the same... one engine is actually producing more energy and power, but that excess power and energy is being consumed by the engine itself... just moving those parts... and in all likelihood, generating much more heat. An F1 engine will be like this... it gets an amazing amount of NET power out of a 3L engine... but it does so by making it spin really fast... that causes it to have to move those internal parts really fast... which means it has to generate a lot of power just to accelerate its own internal parts... and it produces a tremendous amount of heat (which is energy it produces, but just gets wasted... it doesn't help do the work its really trying to do... accelerate the car). Now the F1 engine engineers know all this, so they are trying to minimize the amount of work that gets wasted just moving the engine internal parts. They do that by minimizing the mass of those moving parts and by minimizing the internal friction.
Now, back to EFWUN's statement above. EFWUN is effectively computing the amount of work the engine is doing to move its internal parts. So, if you put two engines on a table, connnected to nothing... and measure how quickly those engines can accelerate from 3000 RPM to 4000 RPM and then to 5000 RPM and so on... THEN you can talk about the amount of horsepower the engine must produce to accelerate its own internal parts. AND EFWUN's calculations that much more work is being done to move those internal parts at 8000 RPM than at 4000 RPM would be absolutely correct...
The flaw is that calculation is telling us how much internal energy the engine must be CONSUMING internally, rather than how much external energy it is PRODUCING to accelerate the car. The rest of us are only focused on what energy the car is PRODUCING.
Now, let me give EFWUN a tiny bit of redemption for his "it depends" answer... if you take two engines producing the same horsepower exactly, though one does it from 3000 RPM to 8500 RPM while the other does it from 6000 RPM to 17000 RPM... and then you put them in identical cars except that you change the final drive ratio by 2x... which car will accelerate faster?
The idealistic answer would say they would be exactly the same. However, that would be wrong. You must consider that in the car whose engine is spinning twice as fast, so is the entire drivetrain from the crankshaft of the engine to the final drive gear... including the clutch and transmission gears. You are having to accelerate those parts twice as much and having to overcome twice as much friction... thus the drivetrain will consume twice the energy. Thus, the higher RPM engine would actually accelerate the car a little less than the lower RPM engine! Thus, there is some value in understanding the work being required just to move the drivetrain parts.
Why did I say "tiny amount of redemption". Well, first because the effect is backwards of what EFWUN's discussions might imply... the higher power at higher RPMs creates LESS acceleration, not more... because he was computing the power loss in the engine/drivetrain, not the power PRODUCED to accelerate the car.
Further, when we measure "engine output", we typically do it with the engine in the car and the car on a dyno. In other words, the car's drivetrain is part of the "engine" we are measuring. Thus, we measure torque and horsepower delivered by the rear wheels to the drum in the dyno. We then typically make adjustments for the approximate 20% energy loss in the drivetrain in order to determine a number for the *engine* horsepower, which is more typically what is quoted (since it is a larger and more impressive number). However, torque and horsepower at the rear wheels is actually far more informative, since it tells us about what we really care about... and reflects a car's superior drive train (if it is lighter weight and/or lower friction).
Hope that helps resolve this thread... and perhaps make it a bit more enlightening in the end. |
rich (Dino2400)
Junior Member
Username: Dino2400
Post Number: 191
Registered: 10-2001
| | Posted on Saturday, April 26, 2003 - 5:50 pm: | |
Tood, I think this might be one such hypothetical posted by EFWUN. I'm only posting this stuff for him because I'm afraid Mitch's behavior has chased him away and I'd like to hear the end of this based on science not let Mitch win just because he chased off all opposition.
------
Efwun (below):
Power equals work/time, which equals work*distance/time. Work equals force times distance, correct? So, if at 4,000rpm,Force is equal to a value of 300, and distance (say the rotation of the crankshaft) is equal to a value of 1, then we have W=300, right? If at 8,000rpm force is equal to 250, and distance (two rotations of the crankshaft) is equal to 2, then W=500, right?
Okay, so, now, let's say time equals 1 (just so we don't have any of that pesky calculus). W/t equals power, right, so let's see, Power at 4,000rpm equals 300units, while Power at 8,000rpm equals 500units.
Then, let's make this all simple for us ignorant slob bastard National Merit Scholar magna grads from Penn, P equals delta KE over time, right? You agreed, right? Okay, so, at 4,000rpm and time equal to 1, P=Delta KE which equals 300units.
At 8,000rpm, P still equals delta KE, right? and let's use the same time unit of 1, just so us simpletons can follow. P=Delta KE which equals 500units. Ooops! There's more of that pesky power to change Kinetic Energy at 8,000rpm than at 4,000rpm!!
------
anything? -Rich |
Todd Wasson (Todd_wasson)
New member
Username: Todd_wasson
Post Number: 7
Registered: 4-2003
| | Posted on Saturday, April 26, 2003 - 5:17 pm: | |
I can't think of a reason why it would do this. If he can post a proof using hypothetical numbers I'd be happy to read it. Until then, I disagree for the reasons posted already.
|
|